Named Entity Recognition using BERT on Subsampled Datasets
The Named-Entity Recognition (NER) system I worked on during my internship at doXray is part of a live production system. At doXray, models in production go through two main phases:
Initial training, which is done on a larger amount of labelled data before the model is deployed to production
Continual learning, which consists of retraining the model, once it is already in production, on a monthly basis with new labelled data alongside the older data.
However, this approach poses some challenges. As new data arrives each month, the total amount of training data is constantly rising, making model training more and more expensive. Furthermore, as with any system in production, there is a possibility of data drift and over time most of the data in the dataset will be older data.
Subsampling in machine learning is a method of reducing the amount of data by selecting a subset of the original data. It is commonly done to resolve class imbalances, but in our case, subsampling was used to combat the aforementioned challenges. By subsampling older data and keeping all newer data, we want to reduce the amount of data and speed up training, while keeping the performance at the same level. Additionally, by prioritising newer, more relevant data, we want to account for data drift.
Dataset
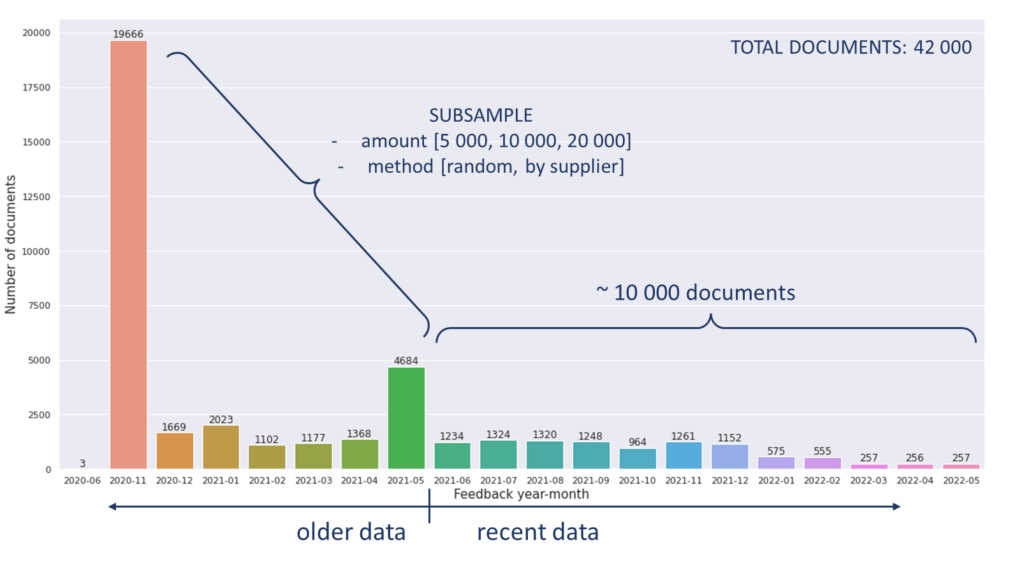
The dataset I used during my internship contains invoice-type OCR scanned documents. There are around 42000 documents in the full dataset, with 10000 of them being recent data (less than 1 year old), and 32000 being older data (more than 1 year old). Each document has information about the supplier of the document and the time it was supplied.
The documents are already split into tokens and each token has a corresponding label. There are 15 labels in total, including the neutral ‘0’ label, which denotes that the token is outside of any named entities. The complete list of entities can be seen in Tables 2 and 3. Unlike the usual IOB-tagging scheme that is widely used for NER tasks, the tags for the beginning and inside of a named entity are not used and each label corresponds to exactly one token.
There are 32 unique document suppliers with 23 of them being present in the older data, and 29 of them in recent data. This suggests that some suppliers are new in recent data, so they will not be represented at all in the older data, but also that some suppliers have been discontinued in recent data.
Another important aspect of the dataset is the number of tokens in different documents. The shortest document length is 48 tokens, the longest is 19599 and the average is 744. As can be seen, document lengths vary greatly, but the average stays roughly the same for both older and recent data. However, this indicates that documents will have to be chunked in order to fit the BERT input, which is 512 BERT tokens.
Dataset Splits
The chart in Figure 1 represents the distribution of labelled documents per month. As can be seen, there is a larger amount of initial training data from November 2020, which is followed by 1000-2000 new documents each month, up to January 2022. Starting from then there is significantly less labelled data. If the model is trained on the full dataset, the recent data is in the minority, which poses a problem because it is likely more relevant in production.
To discover which combination of data works best, the training dataset was first split into recent and older data, with documents older than a year being in the older category, and everything newer than that in the recent category.
The dataset was then subsampled in different ways, with the model trained on the full dataset being the baseline model. Each of the subsampled datasets consists of all recent data, combined with a subsample of older data. Two different subsampling methods were used in combination with three different amounts of data, leading to 6 subsamples.
Data amount
half as many older documents are sampled as there are recent documents
the same number of older documents is sampled as there are recent documents
twice as many older documents are sampled as there are recent document
Subsampling method
documents are chosen randomly
documents are chosen so that there is an approximately equal
number of documents from each supplier
To ensure the validity of the results, all the datasets (including the baseline) were split into five equal parts in which 4/5 were used as a training set and the remaining 1/5 as the validation set (i.e., data was prepared for 5-fold cross-validation). This results in 6 subsampled datasets + baseline dataset = 7 datasets x 5 folds = 35 different datasets to train on.
Data Preprocessing
As mentioned in Chapter 2, BERT expects inputs to be 512 BERT tokens long. However, BERT doesn’t use word tokenization (which is the way data is currently tokenized), but wordpiece tokenization which splits words into subwords. BERT also expects the special tokens [CLS] and [SEP] at the beginning and end of each input. This means that the input can effectively be only 510 wordpieces long. To ensure this is the case, after subsampling the documents in the way described in Chapter 3, the documents were chunked.
The next step in data preprocessing is aligning the original token labels. The original labels align with the original token. However, these tokens have now been split into subwords. There are two common approaches:
propagating the original label to each subword
aligning the label only to the first subword and giving the rest of the subwords the -100 label (which will be ignored when calculating CrossEntropyLoss).
For this task, the second approach was used.
Training and Evaluation
The model used for the experiment was BertForTokenClassification from the HuggingFace Python library, with the ‘bert-base-multilingual-cased’ pretrained model checkpoint.
The training was done using batch sizes of 16, a learning rate of 3e-05 with an Adam optimizer, linear scheduler, and early stopping with a patience of 2. The maximum number of epochs was 15, but this limit was never reached.
To compare the results of models fine-tuned on different subsampled datasets against each other and the baseline, two evaluation datasets were prepared for each of the 5 folds. They consisted of the validation data described in Chapter 3 but filtered to only contain data from the last 6 months for the first set and the last 12 months for the second set. The metric used was the F1-score for each individual entity as well as the macro average of all entities excluding the neutral ‘0’ label. To calculate the final metrics for every dataset, the scores for each of the 5 folds were averaged.
Results
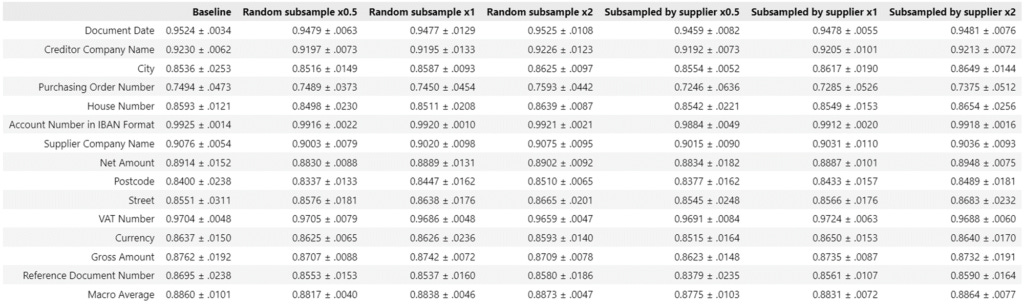
Table 1 shows the macro F1-score average on 6-month and 12-months-old evaluation data as well as the average best epoch and the approximate time needed for one epoch in minutes.
As can be seen from Table 1, all results are very similar, with the general trend being that more data leads to very slightly better F1-scores and that models achieve slightly better F1-scores on 6-month evaluation data than on 12-month evaluation data. For 6-month evaluation data, both biggest subsampled datasets outperform the baseline in terms of F1-score, but only by a very thin margin. For 12-month evaluation data, the baseline remains the model with the highest F1-score. The biggest difference in the datasets is in their training time, with the smallest of the models needing less than half the training time needed for the baseline.
Important to note here is that datasets that were subsampled according to the supplier are slightly smaller than the ones subsampled by random, due to some suppliers having slightly fewer documents than were necessary for a completely equal split between all suppliers. The shorter training times are therefore to be expected.
Table 2 and Table 3 offer more detailed results, showing F1-scores for each individual entity. These results also show very similar results between all subsampled datasets, with none of the entities experiencing a significant performance drop or rise.
Conclusion
The main task of this internship was to find a way to reduce the amount of older training data in a way that, when used to train a new model, would maintain the F1-score of the baseline but lower the training time. This was done by creating 6 different subsampled datasets and using each one to train a BERT model, along with a baseline. These models were then compared against each other. The results showed a very small decrease in F1-scores (at most a 0.011 decrease) for datasets with a much smaller number of data (the smallest of which is around 35% of the size of the full dataset). Similarly, no notable difference was found between subsamples created at random and the subsamples created by sampling the same number of documents from each supplier.
In conclusion, subsampling older data in any of the ways tested during this internship offers a faster training time and minimal cost with respect to the F1-score.






The data drift challenge really hit home. Smart approach to cosst.